Are dividends more important than earnings for stock valuation?

Last week, I ragged on earnings per share (EPS). Today, I want to be more constructive.

If we shouldn’t rely on EPS for valuation, what should we rely on? If not EPS, then what?

How about dividends?

Cash is fact, profit an opinion

Over three decades ago, economist Alfred Rappaport wrote the classic Creating Shareholder Value.

In it, Rappaport wrote that cash is a fact, profit an opinion.

Many have propagated that message since, including his future collaborator Michael Mauboussin.

(By the way, Mauboussin should get some honorary title for services rendered to the investment community for the bulging catalogue of free investment papers he’s published over the years.)

British economist John Kay was another messenger, writing:

‘Most thoughtful analysts look at cash flow and assets rather than reported earnings when they try to assess the fundamental value of a business.’

So if cash is more informative than earnings, how can investors use cash flows to improve their stock analysis?

A hasty way is to overcome the unreliability of EPS by tethering earnings to cash flow. Anchor earnings to cash and see if you can spot any suspicious divergence.

As Kay again wrote:

‘Cash is a good reality check. A common feature of all the accounting wheezes…is that increased reported earnings have no cash counterpart. Tax is also a clue to what is really going on. Revenue authorities have many faults, but they do not often levy tax on profits that do not exist.’

High profits and a low tax charge may mean that profits are not what they seem.

We can go beyond using cash flows as a check on earnings, however. Cash can be used as the key input to value stocks.

Dividends as proxy for cash flows and value

If cash is a better measure than EPS, we can use dividends per share (DPS) as a proxy for cash flow. 

After all, what are dividends if not a company’s cash flow accruing to shareholders?

One way to value a stock using dividends is via the dividend discount model, which calculates the sum of the present value of all future expected dividends issued to shareholders.

John Kay is useful again here, expounding a simple way to use the model:

‘If 5% growth [of dividends] is the long-term average, there is a simplifying trick. Subtract 5%, the growth rate, from 8%, the discount rate [we can choose a different discount]. The difference, 3%, should be the dividend yield on the share.’

Kay's simplifying 'trick' has a fancier name -- the Gordon growth model, which has the following formula: 

Stock price = DPS/(r - g)

In the formula: 

DPS = expected dividends per share a year from now 
r = required rate of return for investors/discount rate 
g = stable, long-term dividends growth rate  

Commonwealth Bank example 

Let's use Commonwealth Bank of Australia [ASX:CBA] as an example.

CBA’s FY24 DPS is expected to be $4.36 a share.

Using a discount rate of 8% and a (high) stable growth rate of 5%, we get a valuation of $145 a share, well overshooting the current price of around $102.

I won't be rushing to buy CBA shares just yet, though. A growth rate of 5% seems excessive for a mature firm like CommBank. 

We can work backwards using the formula to figure out what the market’s implied growth rate is for the bank: 

$102 = $4.36/(8% - g) 

Solving for g gets us a stable growth rate as implied by the current price of about 3.7%

More reasonable, but still a bit of a stretch given the lower growth of the Australian economy. 

A stock's stable growth rate has to be less than or equal to the growth rate of the economy in which it operates. 

In the May Statement on Monetary Policy, the Reserve Bank projected GDP growth to be below 2% well into 2025. 

Using 2% as a stable growth rate, we get a valuation for CBA of around $73 a share. Using a growth rate of 3%, we get $87. 

Clearly, the model is highly susceptible to suggestion. (But the more down-to-earth growth rates do seem to hint the bank's valuation is stretched). 

Tweak a key input like the growth rate, and the valuation fluctuates. 

Pitfalls of the dividend discount model 

The dividend discount model has great intuitive appeal. And it references cash flows (via dividends) instead of earnings!

Surely, it’s the perfect measure of a stock’s value then, right?

Unfortunately, nothing is so straightforward in investing.

The model has its downsides.

The biggest, already mentioned, is the sensitivity to assumptions. 

Finance professor Aswath Damodaran explained it well when he wrote: 

‘The model is a simple and convenient way of valuing stocks but it is extremely sensitive to the inputs for the growth rate. Used incorrectly, it can yield misleading or even absurd results, since, as the growth rate converges on the discount rate, the value goes to infinity. Consider a stock, with an expected dividend per share next period of $2.50, a cost of equity of 15%, and an expected growth rate of 5% forever. The value of this stock is $25.00. Note, however, the sensitivity of this value to estimates of the growth rate.
‘As the growth rate approaches the cost of equity, the value per share approaches infinity. If the growth rate exceeds the cost of equity, the value per share becomes negative.’

Damodaran then shared this very good chart to illustrate the model’s hypersensitivity (using his previous example as the base):

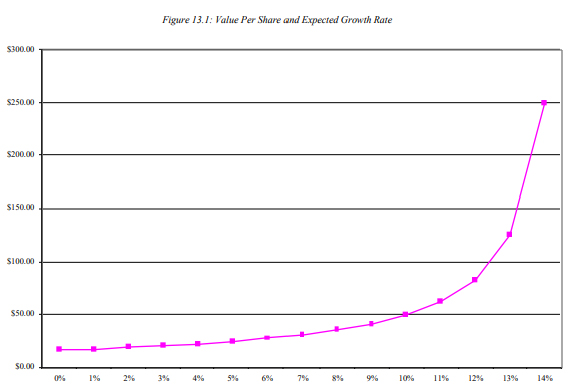
The model is intuitive and uses cash flows as inputs. But it cannot escape the perils of relying on assumptions.

The model and the payout 

Another thing to consider is a stock's payout ratio (the percentage of earnings dished out as dividends). 

The model focuses on dividends so how does it deal with a firm whose payout ratio is negligible? 

My What's Not Priced In co-host Greg Canavan raised this issue. 

If a stock has a payout ratio of 10%, dividends are only a small portion of its total return. So should the model treat this firm the same as a firm with a payout ratio of 70%? 

Aswath Damodaran shared Greg's concerns, conceding this about the Gordon growth model: 

'The dividend payout of the firm has to be consistent with the assumption of stability, since stable firms generally pay substantial dividends. In particular, this model will under-estimate the value of the stock in firms that consistently pay out less than they can afford and accumulate cash in the process.' 

(By the way, Greg just published a report detailing his top six dividend plays on the ASX right now. Greg's criteria wasn't traditional though: he emphasized growth first, income second.)

Damodaran did suggest a workaround. 

You can recalibrate the growth rate to the stock's payout ratio. Damodaran suggests doing it this way: 

growth rate = (1 - payout ratio)*ROE 

Let's apply that to Commonwealth Bank again. 

Commonwealth Bank example, redux 

Let's crudely use the FY24 EPS and FY24 DPS to come up with CBA's payout ratio. 

Consensus forecasts have CommBank's FY24 EPS hitting $5.83 and FY24 DPS hitting $4.36, giving a rough payout ratio of 75%. 

The bank's FY24 ROE is forecast at 13%. 

So, plugging Damodaran's workaround gives us a growth rate of (1-0.75)*0.13 = 3.25%. 

Interesting! A little under the market's implied rate of 3.7%. 

To complete the example, let's use the 3.25% growth rate to come up with a final valuation for CBA: 

$4.36/(8%-3.25%) = $92

Under this model, CBA is 10% overvalued. 

The analyst’s plight — no shortcuts in sight

Investors must resist the temptation to seek shortcuts and analytical paths of least resistance.

Quickly checking the EPS or the P/E multiple is easy. But is it worthwhile?

Not really.

Investing is a competitive game where the shortcuts lead nowhere but average returns … or worse.

Martin Fridson put it best in his magnum opus, Financial Statement Analysis (my emphasis):

‘Financial reporting occurs in an institutional context that obliges conscientious analysts to go many steps beyond conventional calculation of financial ratios. Without the extra vigilance…the user of financial statements will become mired in a system that provides excessively simple answers to complex questions.’

P.S. Again, if you're interested in Greg's dividend ideas, you can read his analysis here!