Demystifying Interest Rate Duration

Many investors approach fixed income markets with a sense of trepidation as the concepts underlying them appear somewhat arcane. Partly this is due to the nature of fixed income investments and the more formalised dynamics and relationships which drive their returns. What follows is a series of primers outlining the key concepts behind fixed income dynamics and portfolio management to assist in demystifying the fixed income markets. The first instalment of this series shall have a closer look at the concept of interest rate duration (‘duration’).

Defining Duration

Duration brings together a range of factors which summarise in a single number the sensitivity of a bond to a change in yields. Duration is therefore quite distinct from Term to Maturity which measures the length of time until the principle of the bond is repaid. Conveniently when dealing with duration these numbers are additive so that the duration of a portfolio of bonds is simply the weighted average of the duration of the individual bonds.

Potentially confusing for investors is that there are several ways that duration can be quoted. Often duration will be quoted in terms of years though it may also be quoted as a percentage. While at the margin there are mathematical differences between the methodologies underlying the different forms of quotation in everyday practice it is safe to assume that the two formats are analogous. This means that the utilisation and interpretation of duration by investors as a measure is unaffected by the form in which it is quoted. For convenience, as it aligns more closely with how investors think of the term to maturity of a bond, it is often most intuitive to refer to duration in terms of years.

Quantifying Duration

There are several ways for an investor to measure duration and the interpretation will vary subtly based on the measure utilised. Despite the subtle differences in interpretation the common factor behind all measures of duration is that they seek to quantify the impact on the value of a bond from parallel shifts in the yield curve; i.e. movement in yields is the same across the entire yield curve.

Macauley Duration: This measure of duration is the weighted average of the time to receive the cashflows from a bond and is measured as years. This measure of the level of interest rate sensitivity of a bond measures the weighted average time that a bond needs to be held so that the total present value of the cash flows from the bond equals the current market value of the bond.

Modified Duration: Modified duration measures the sensitivity of the value of a bond to a small change in the yield of the bond. It is effectively the first derivative of the bond pricing formula for a change in yield and is typically measured as a percentage. Though utilising different calculations Macauley and Modified duration end up being quite similar in terms of results. Indeed, the Modified Duration can be calculated by a suitable adjusting to the Macauley Duration namely dividing Macauley Duration by 1 plus yield to maturity (divided by number of coupons p.a.).

The limitation of Modified Duration as a measure is that it assumes small changes in yield typically of 1 bp. This can create issues where the price relationship between yield and bond price is non-linear for larger movements in yields.

Effective Duration: To overcome this limitation effective duration is often calculated. As with Modified Duration, Effective Duration measures the sensitivity of a bond price to changes in yields with the key differences being (a) each cash flow is valued based on movements in the entire yield curve and (b) more material changes in yields, such as 25bps or more, are utilised in the calculation of changes in prices. The difference in calculations becomes more relevant where bond pricing exhibits material levels of non-linearity due to optionality within the structure. Accordingly, Effective Duration measures the sensitivity of a bond’s price to material movements in the entire yield curve.

Interpreting Duration

Despite the different approaches to calculating duration, for investors in traditional vanilla bonds the results derived from the three measures is usually very similar. The reason for this is that the major factor which creates differences between the calculations is non-linearity in the price of a bond to changes in yields. In turn such non-linearity is normally a result of some form of optionality embedded within the bond structure which is absent from traditional vanilla bonds.

Irrespective of the measure of duration utilised by the investor the relationship between the price of the bond and changes in the yields is :

∆ Value _Bond ≈ - Duration _Bond * ∆ Yield _Bond

It is apparent from the calculation that the relationship between the value of a bond and yields is negative; e.g. as yields rise the value of a bond declines. Logically this relationship follows as a bond is a fixed set of cash flows providing a set yield if held to maturity. Given the set nature of cashflows as yields rise the value of the bond must decline so that the cumulative value of the cashflows equates to the higher yield now demanded in the market; i.e. the present value of the cash flows from the bond declines. The opposite holds if yields decline. The relationship also highlights that the greater the duration of a bond the greater the impact from changes in yields. It is due to these relationships that active duration management is often utilised as a key source of active management within bond portfolios.

What Factors Impact on the Duration of a Bond?

The duration of a vanilla bond is determined by a number of factors which include :

- Term to Maturity

- Coupon

- Yield

As these factors will vary between bonds and over time so too will the duration of bonds vary at a point in time and over time. When considering the impact on the duration of a bond it is useful to view duration as analogous to a pivot point balancing a ‘seesaw’. Spread out across the seesaw are all the cash flows earned over the life of the bond with the dominant one being the repayment of principal, also referred to as face value, on maturity. The duration, or pivot point, moves back and forth to maintain the balance between cashflows so that the seesaw is always level.

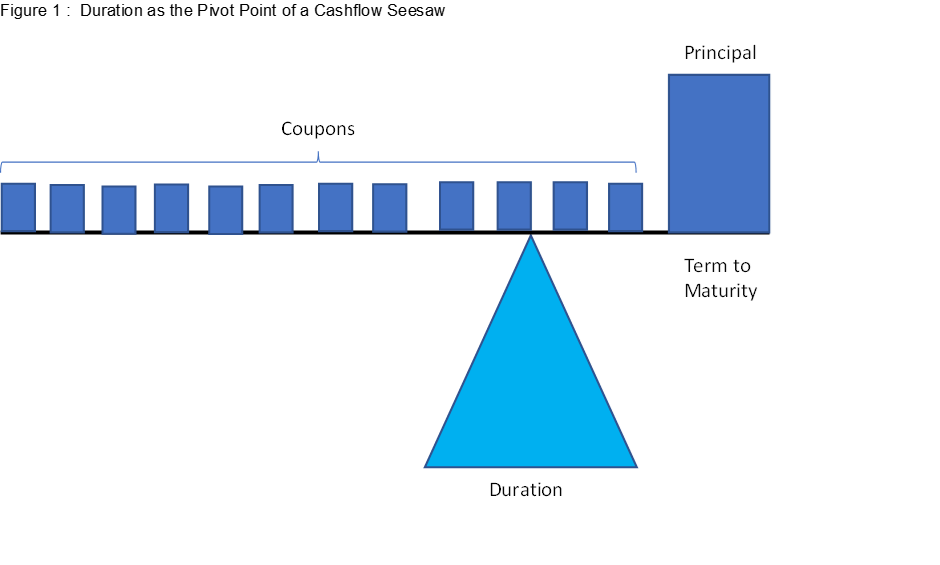
Such a visual conceptualisation of duration can assist in understanding how duration changes as the underlying factors change. To illustrate consider the impact of a rise in yields. As yields rise the present value of all the cash flows declines but the impact to the right of the pivot point, due to the principal, is materially greater than that to the left. To prevent the seesaw from leaning to the left the pivot point, or duration, must move to the left; i.e. yield and duration are negatively related so duration shortens. Working through similar thought exercises it follows that duration is also negatively related to size of coupons and positively related to Term to Maturity.

Duration measures one of the cornerstone risks within securities and fixed income portfolios. Understanding duration is accordingly one of the key aspects of appreciating the different aspects associated with managing the risk within a fixed income portfolio.