Doing the maths on diversification
Risk is one of the biggest disadvantages we all face in growing and protecting our wealth. In the world of investing there are two types of risk:
Systematic risk or market risk which are risks such as inflation, COVID-19, the Global Financial Crisis, geo-political risks (wars etc) and the broad macroeconomic environment. Systematic risk is unavoidable as it can affect wide-spread assets, markets and sectors. It is also unpredictable, no one saw COVID coming, nor war in Eastern Europe.
The second type is non-systematic risk. These are more specific risks or micro risks of investing. Non-systematic risk is caused by actions or events from specific industries, investable firms or investment strategies. The good news for investors is non-systematic risk can be placated with diversification.
Diversification helps us with our decision making when it comes to portfolio creation and allocation. It can reduce risk in your portfolio, smooth out returns and preserve your capital during market downturns.
With that, this wire will discuss the method that proves diversification works in order to mitigate non-systematic risk.
Modern Portfolio Theory
For those that have not come across Harry Markowitz he is the founding father of Modern Portfolio Theory (MPT) for which he won a Nobel Prize. MPT theorised that combining two or more complementary assets can optimise returns for any level of risk.
This has given rise to diversification strategies such as the 60:40 portfolio, blending assets and even creating specific risk portfolios that blend everything from international equities to bonds to property to cash.
Statistics and portfolio construction
The mathematics of MPT falls into the realm of statistics and the use of standard deviations, expected returns and time. Using these variables Markowitz developed the concept of the ‘efficient frontier’.
What the efficient frontier is designed to do is compare the returns of each asset held over the same period of time across different allocation levels and risks.
Using MPT to design a portfolio
Let’s use the ASX 200 ETF IOZ and the Australian Bond ETF IAF as an example. Here is the yearly performance of IOZ and IAF over the past 10 years:
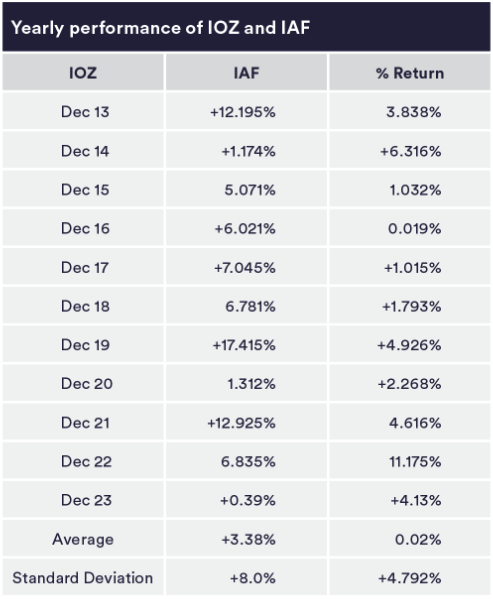
Source: Refinitiv Datastream/InvestSMART
What you will notice is that the risk in IOZ is higher than IAF with much higher intra-year movements. This is what should be expected, as equities are riskier than bonds. To ‘judge’ this risk we also need to apply a standard deviation (SD) to the returns.
Standard deviation between asset classes
The SD represents the average dispersion from the mean. It is a standard measure of risk. In the case of the IOZ and IAF, the statistical movement of IOZ would be between -4.62% (3.38% – 8.0%) and +11.38% (3.38% + 8.0%) assuming a standard distribution. For IAF the statistical movement would be between -4.99% (-0.2% – 4.79%) and +4.59% (-0.2% + 4.79%) also assuming a standard distribution.
The next step in the maths of diversification is to combine IOZ and IAF into a portfolio to see if the standard deviation of a combined holding is less than either of the individual standard deviations of IOZ and IAF.
This requires us to use a multiple asset portfolio formula to calculate SD of combined holdings and using a ‘covariance’ measure. Covariance is a measure of how changes of one variable are associated with the changes of a second variable. In other words, covariance quantifies how closely two assets move in tandem.
Let’s combine IOZ and IAF into hypothetical portfolios...
The first portfolio holds 100% IOZ and 0% IAF. The weights slide by 10% each time for the final portfolio to hold 0% IOZ and 100% IAF. The combined returns are:
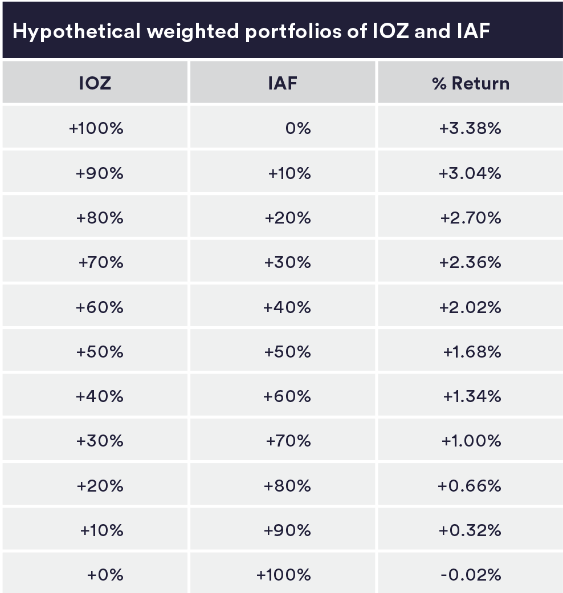
The return is the combined capital yearly average. When we apply a combined standard deviation to this with a risk weighted ratio it turns out that a portfolio with the optimal weighting is the 70:30 IOZ:IAF portfolio.
If we chart this you can see that the 70:30 portfolio isn’t as volatile as just holding IOZ, but returns are more optimal than holding just IAF.
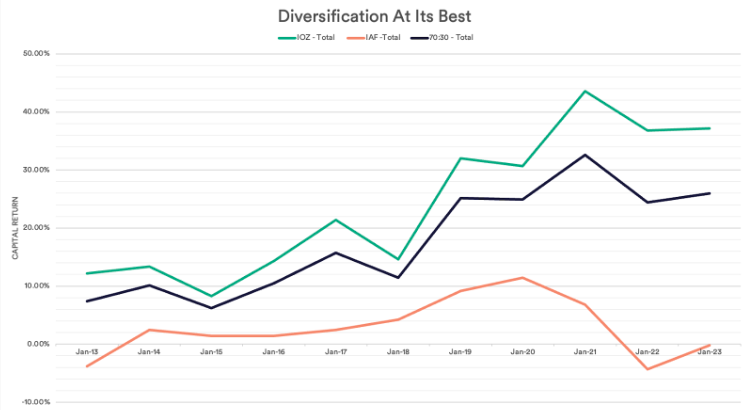
Smoother returns – the 60:40 sweet spot
We can take this a step further, as the more assets you combine using the mathematics of diversification the smoother the volatility. This is where risk is important. Although a 70:30 portfolio might be optimal from a maths perspective, from a behavioural perspective investors’ risk tolerance is generally lower. All that is required is to move down the risk tolerance to the next optimal return, this is: 60:40 equity to bonds.
If we take that optimal risk profile and add extra asset classes such as cash, property and international equities and use a 55:45 ‘balanced portfolio’ the return looks as follows.
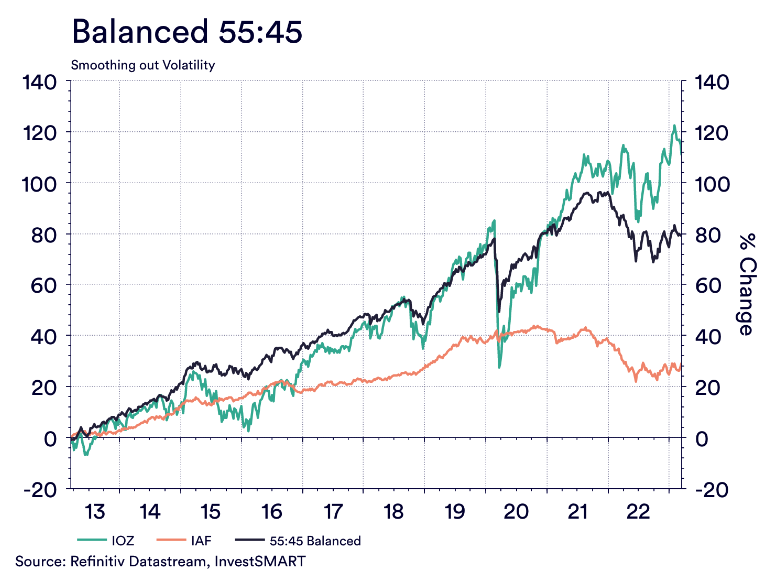
The individual variances are smoothed out and the impacts of non-systematic risks are negated. The 55:45 weighting can even absorb the systematic risk of global events like COVID-19 and the war in Ukraine with smaller declines to these large events.
The conclusion to be drawn is that diversification works as the maths and real-world examples prove. It is why Harry Markowitz won a Nobel Prize for it and why portfolio managers like us use it as the basis for all good portfolio creation and asset management.
3 topics
.png)
.png)